月: 2021年7月

★ 本記事のテーマ

分布に関係なく、確率密度関数があります。その特徴は何でもよいですが、

何でもいいので、確率密度関数という難しい言葉へのアレルギーを回避しましょう。

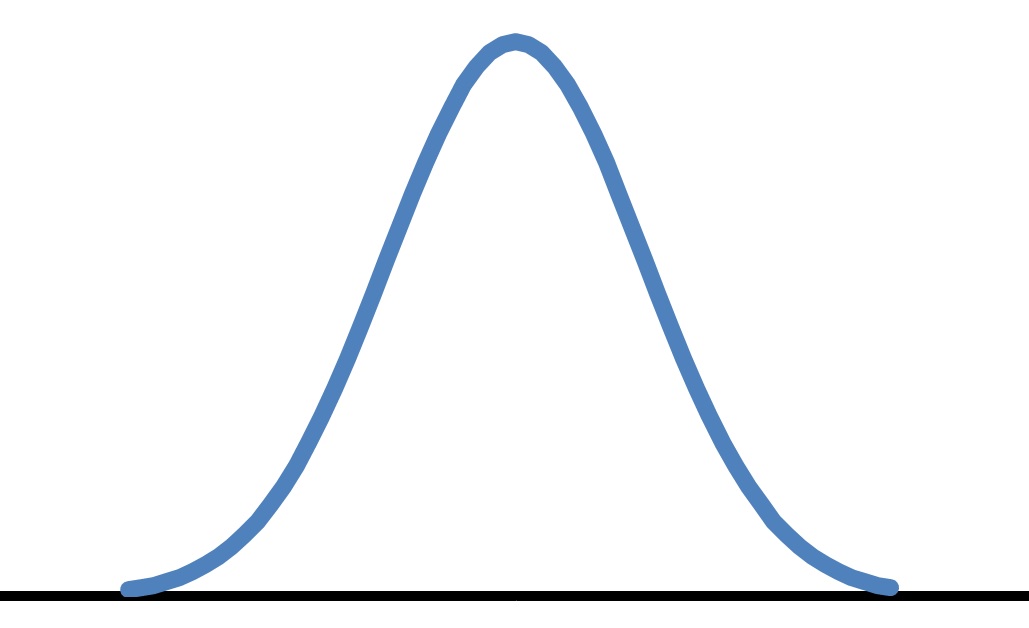
\(f(x)=\frac{1}{2500}(-(x-50)^2+2500)\)
\(f(x)=\frac{1}{2} e^{|x|}\)

グラフを描いてみましょう。分布関数の感じが出て、その関数の全区間の積分値が1となっています。

これが確率密度関数です。

●確率は、∫f(x)dx　です。
●期待値E[X]は E[X]=∫xf(x)dx です。
またE[X²]=∫x²f(x)dx です。
●分散はV[X]=E[X]²– E[X²]です。

●You tube動画もあります。ご確認ください。

●You tube動画ご覧ください。

いきなり、

がすぐわかる例題を紹介します。

期待値の計算方法は、確率×出る目の合計ですよね。
(1)期待値E=\(\frac{1+2+3+4+5+6}{6}\)=\(\frac{21}{6}\)=3.5
(2)出る目と確率を整理しましょう。

期待値E=\(\frac{2×1+3×2+・・・+12×1}{12}\)
=7
また、１個の目の期待値の倍としてもよいですね。

統計の難解な数式に早く慣れる方法を提案します。数学の得意・不得意関係なく、数式の意味を読み取るには結構時間がかかります。よく使う方法が２つあります。

★難しい数式の読み方

先の、サイコロ１との出る目の期待値の計算は。
E=1×\(\frac{1}{6}\)+2×\(\frac{1}{6}\)+・・・+6×\(\frac{1}{6}\)
=\(\frac{21}{6}\)=3.5
ですね。数字1から6は｢出る目｣の値で、\(\frac{1}{6}\)は確率ですね。

出る目を\(x_i\)、出る目\(x_i\)の確率を\(p_i\)、和をΣで書き直します。

ここで確率\(p_i\)を確率密度関数f(x)に変えて定義することもあります。その場合、2つ定義を変えます。

期待値Eは
●E=\(\int xf(x) dx\)
となります。∫も関数も出てきましたが、基本は
●E=\(\sum_{i=1}^{n} x_i p_i\)
です。見た目は違いますが、サイコロの出る目の期待値を求める式と同じです。

★期待値の加法性

加法性に慣れるポイントについて、
具体的な例で理解しましょう。期待値の基本はサイコロの出た目の計算ですね。

➀は(\(1×\frac{1}{6}\)+・・・+\(6×\frac{1}{6}\))=\(\frac{21}{6}\)=3.5
を3倍しますから、3.5×3=10.5です。

②は(\(1×\frac{1}{4}\)+・・・+\(4×\frac{1}{4}\))=\(\frac{10}{4}\)=2.5
を2倍しますから、2.5×2=5です。

さらに5を足すので、期待値は10.5+5+5=21.5です

一方、期待値の加法性を使うと、
●E=E[aX+bY+c]
に、a=3,b=2,c=5,E[X]=3.5,E[Y]=2.5を代入します。
●E[aX+bY+c]=aE[X]+bE[Y]+c=3×3.5+2×2.5+5=21.5
と結果が一致します。

期待値の加法性の公式を使ってもよいし、サイコロの出る目の式のまま解いてもよいのです。
慣れないうちはサイコロの出る目の計算で
慣れたら一般化の式を理解していきましょう。

★期待値の加法性がわかるポイント

期待値の加法性に少し慣れたら、次の計算をしてみましょう。

➀は加法性で出たE[aX+bY+c]=aE[X]+bE[Y]+cを使えばよいです。でも、E[\(X^2\)]はどうしましょうか？ 抵抗感がありますが、次の例題で解決します！

➀は(\(1×\frac{1}{6}\)+・・・+\(6×\frac{1}{6}\))=\(\frac{21}{6}\)=3.5ですね。
②は機械的にそのまま2乗を式に入れます。

E[\(X^2\)]=(\(1^2×\frac{1}{6}\)+・・・+\(6^2)×\frac{1}{6}\)
=\(\frac{(1+4+9+16+25+36)}{6}\)
=\(\frac{91}{6}\)ですね。

\(x^2\)の期待値とはどういう意味か？が気になりますが、あまり気にしないで代入してください。

ですから、E[\(X^3\)]を求めようとすると、
E[\(X^3\)]=(\(1^3×\frac{1}{6}\)+・・・+\(6^3×\frac{1}{6}\))となります。

出る目Xを変数にして、いろいろな変数を代入することに慣れてください。ここが分散の導出に必要です。期待値Eはサイコロの出る目の計算であることは変わりませんが、E[X]に変数Xをいろいろ代入するように慣れていきましょう。

★分散の定義

上の式が理解するための3つのポイントを解説します。

★分散の定義で理解したポイント

★(A)E\((X-E[X])^2\)の意味

分散の定義は、各データと平均との差を2乗した和を個数で割る値ですね。式で書くと、
\(V=\frac{(x_i-μ)^2}{n}\)
になります。

ここで、
(あ)\(x_i\)をX
(い)μをE[X]に変え、
(う)全体の\(\frac{1}{n}\)は平均Eとすると、
\(V=\frac{(x_i-μ)^2}{n}\)
=\(\frac{(X-E[X])^2}{n}\)
=E[\((X-E[X])^2\)]
に変えることができます。

(あ)(い)は文字を変えるだけで理解しやすいです。(う)は理解しづらいので解説します。

個数nで割るは、全体を平均値とすると同じですね。なので、全体に期待値E[]をつけることになります。

★(B)\(E[X^2]-E[X]^2\)になる理由

次で解説します。

E[X]に慣れるために、教科書やwebサイトのように途中経過を省かずに計算します。

V[X]
=E[\((X-E[X])^2\)]
=E[\(X^2-2XE[X]+E[X]^2\)]
ここは、\((x+y)^2=x^2+2xy+y^2\)です。
=E[\(X^2\)]-E[2XE[X]]+E[\(E[X]^2\)]

各項をばらばらにしました。
さて、ここでE[X]は平均値μで、変数ではなく定数ですよね。
=E[\(X^2\)]-E[2Xμ]+E[\(μ^2\)]
=E[\(X^2\)]-2μE[X]+\(μ^2\)
平均値μは定数なので、E[]の外に出せます。

さらに、定数μ=E[X]に戻します。ここの変形が強引ですけど。
=E[\(X^2\)]-2 E[X]E[X]+\( E[X]^2\)
= E[\(X^2\)]-\( E[X]^2\)
よって、
V[X]= \(E[X^2]-E[X]^2\)

分散の導出過程をよく見て、期待値E[X]、E[\(X^2\)]アレルギーを無くしていきましょう。ここがクリアーすれば、回帰分析、分散分析、検定などの理解が早くなります。

では、いくつか演習問題を解いて、公式に慣れましょう。

という感覚でOKです。

【解】大学入試で出題された問題です。実際に書き出して、期待値と分散を計算します。

上表をもとに、数列を使って期待値、分散を計算します。

●期待値E(X)は
E(X)=1・\(\frac{2}{10}\)+2・\(\frac{1}{10}\)+3・\(\frac{2}{10}\)+4・\(\frac{1}{10}\)+5・\(\frac{2}{10}\)+7・\(\frac{1}{10}\)+9・\(\frac{1}{10}\)=4

●分散V(X)は
V(X)=\((1-4)^2\)・\(\frac{2}{10}\)+\((2-4)^2\)・\(\frac{1}{10}\)+\((3-4)^2\)・\(\frac{2}{10}\)+\((4-4)^2\)・\(\frac{1}{10}\)+\((5-4)^2\)・\(\frac{2}{10}\)+\((7-4)^2\)・\(\frac{1}{10}\)+\((9-4)^2\)・\(\frac{1}{10}\)=6

数列を使った１問でした。

サイコロの問題は超有名なので、是非解きましょう。

1つ目のサイコロの目と２つ目のサイコロの目の出方はそれぞれ独立とします。
●E(X)=\(\frac{1}{6}\)(1+2+3+4+5+6)=\(\frac{7}{2}\)
●E(X²)=\(\frac{1}{6}(1^2+2^2+3^2+4^2+5^2+6^2)\)=\(\frac{91}{6}\)
●E(X)E(Y)=E(X)E(Y)= \(\frac{49}{4}\)
を使って問を解きます

(1)
● E(X+Y)=E(X)+E(Y)= \(\frac{7}{2}\)+\(\frac{7}{2}\)=7
●E((X+Y)²)=E(X²)+2E(X)E(Y)+E(Y²)
= \(\frac{91}{6}\)+2・\(\frac{7}{2}\)・\(\frac{7}{2}\)+ \(\frac{91}{6}\)= \(\frac{329}{6}\)
●V(X+Y)= E((X+Y) ²)- E(X+Y) ²
=\(\frac{329}{6}\)-49=\(\frac{35}{6}\)

(2)
● E(XY)=E(X)E(Y)= \(\frac{7}{2}\)・\(\frac{7}{2}\)=\(\frac{49}{4}\)
●E((XY)²)=E(X²)・E(Y²)= \(\frac{91}{6}\)・\(\frac{91}{6}\)= \(\frac{8281}{36}\)
●V(XY)= E((XY)²)- E(XY) ²=\(\frac{8281}{36}\)-\(\frac{2401}{16}\)=\(\frac{11515}{144}\)

機械的に計算しながら、公式や数列の計算に慣れていきましょう。

【問3】、【問4】は積分の演習問題です。

高校数学ですね。簡単な式で期待値、分散の積分計算に慣れていきましょう。

(1) \( \displaystyle \int_{-3}^{3} f(x)dx \)=\( \displaystyle \int_{-3}^{3} \frac{1}{36}(-x^2+9)dx \)
=\(\frac{1}{36}\)\(\left[ -\frac{1}{3}x^3+9x \right]_{-3}^{3}\)=1
全区間の積分、つまり、全確率は合計１です。そりゃ、そうですよね！

(2)
●E[X]= \( \displaystyle \int_{-3}^{3} xf(x)dx \)=\( \displaystyle \int_{-3}^{3} \frac{1}{36}x(-x^2+9)dx \)
=\(\frac{1}{36}\)\(\left[ -\frac{1}{4}x^4+\frac{9}{2}x^2 \right]_{-3}^{3}\)=0
となります。確かにy軸に対象な関数なので、平均は0ですね！確かに！

●E[X²]= \( \displaystyle \int_{-3}^{3} x^2f(x)dx \)=\( \displaystyle \int_{-3}^{3} \frac{1}{36}x^2(-x^2+9)dx \)
=\(\frac{1}{36}\)\(\left[ -\frac{1}{5}x^5+3x^3 \right]_{-3}^{3}\)=\(\frac{9}{5}\)
より、
●V[X]= E[X²]―E[X] ²=\(\frac{9}{5}\)

積分慣れていきましょう。
●E[X]= \( \displaystyle \int_{a}^{b} xf(x)dx \)
●E[X²]= \( \displaystyle \int_{a}^{b} x^2 f(x)dx \)
を定義どおり、積分すれば確率・期待値・分散は計算できます。

(1)は離散系なので数列∑、(2)は連続系なので積分を使います。同じ問題ですが、連続系と離散系で計算結果が若干変わる点が面白いので、解いてみましょう！

(1)
●期待値E=\(\sum_{i=1}^{n} i \frac{1}{n}\)=\(\frac{1}{n} \frac{1}{2}n(n+1)\)=\(\frac{1}{2}(n+1)\)
●分散V＝\(\sum_{i=1}^{n}\frac{1}{n}(i-\frac{n+1}{2})^2 \)=\(\frac{1}{12}(n+1)(n-1)\)

(2)
●期待値E=\( \displaystyle \int_{0}^{n} xf(x)dx \)=\( \displaystyle \int_{0}^{n} x \frac{1}{n})dx \)=\(\frac{n}{2}\)
●分散V＝E(X²)-E(X) ²=\( \displaystyle \int_{0}^{n} x^2 f(x)dx \)-\((\frac{n}{2})^2\)=\(\frac{n^2}{12}\)

表にすると、離散系と連続系で結果が若干かわります。

以上、数列・積分を使って、確率・期待値・分散が計算できることを確認しました。

「確率変数の期待値と分散が計算できる【初心者向け】」を解説しました。

★ 本記事のテーマ

さっそく見ていきましょう。

●You tube動画もご確認ください。

正規分布の標準化とは、平均0、分散\(1^2\)に直すことです。数式では、平均μ(≠0)、分散\(σ^2≠1^2\)な正規分布を次の式で標準化します。

$$ Z=\frac{\bar{x}-μ}{σ} $$

　標準化した場合のグラフの変化イメージを見ましょう。平均10,分散\(5^2\) (以下N(10,\(5^2\))と書きます)の正規分布を標準化した場合の図です。正規分布は平均、分散によって尖り具合が違いのがわかります。

正規分布の標準化する理由は、正規分布表が1つで済むからです。わかっているなら簡単ですが、そうでない場合は、理由をわからずに標準化の式を使っていることになり、注意が必要です。

世の中には、いろいろな平均・分散から成る正規分布がたくさんあります。
【簡単】正規分布は怖くない！正規分布表や確率計算の求め方がすぐわかるにあるように、正規分布は積分が困難な関数なので、正規分布表を作っていましたね。

あらゆる平均、分散に対して正規分布表を作ると大変になります。だから、平均0、分散\(1^2\)に直します。そうすれば、平均0、分散\(1^2\)の正規分布表１枚で済みますよね。

標準化する理由を理解した次は、いろいろな応用問題に振り回されずに済む必勝方法を解説します。

数学が得意で正規分布に慣れた私でも、出題された瞬間、手が止まります。でも安心！必勝方法に持ち込めば解けます！ その方法は次の3つです。簡単な問いでも難しい問いでも必ず3つの方法で解いていきます。

次に、資格試験に頻出な応用問題を例に必勝解法で攻略します

3題挙げます。

これならできそう

ちょっと応用

かなり応用、手ごわい

重要なのは、どんな問いが出ても次の3つの方法で攻略すれば解けます!

正規分布のなめらかなグラフを描きます。

正規分布の①P(X＜15)、②P(X≦3)、③P(12≦X≦14)、④P(5≦X≦11)区間を斜線で塗りましょう。

なめらかなグラフを描きます。

Z=\(\frac{μ-\bar{x}}{σ}\)=\(\frac{μ-10}{5}\)を代入します。結果は上図のKpになります。
ここまで、機械的に絵を描けば、どの面積を出せば良いかがはっきりしますね。面積は正規分布表から値を求めます。

➀はKp=1以上の面積ですから正規分布表Kp=1のpが答えです。よって、p=0.1587
②は左右対称性で考えれば、Kp=1.4以上の面積ですから正規分布表Kp=1.4のpが答えです。よって、p=0.0808
③はKp=0.4以上の領域から、0.8以上の領域を引けばよいですね。よってp=0.3446-0.2119=0.1327
④はKp=-1から0までの領域と、0から0.2までの領域に分けます。
Kp=-1から0までの領域は、左半分確率0.5からKp=-1以下の領域を引けばよいですね。
Kp=0から0.2までの領域は右半分確率0.5からKp=0.2以上の領域を引けばよいですね。
よって答えは　(0.5-0.1587)+(0.5-0.4207)=0.4206

正規分布表はこの4パターンが図から計算できれば完璧です！

正規分布のなめらかなグラフを描きます。

正規分布の①P(X>180)、②P(160≦X≦175)区間を斜線で塗りましょう。

なめらかなグラフを描きます。

Z=\(\frac{μ-\bar{x}}{σ}\)=\(\frac{μ-170}{6}\)を代入します。結果は上図のKpになります。
ここまで、機械的に絵を描けば、どの面積を出せば良いかがはっきりしますね。面積は正規分布表から値を求めます。

➀はKp=1.66以上の面積ですから正規分布表Kp=1.66のpが答えです。よって、p=4.85%
②は160cm(Kp=-1.66)から170cmまでの確率と170cmから175cm(Kp=0.83)までの確率を求めたらよいですね。
Kp=-1.66から0までの領域は、左半分確率0.5からKp=-1.66以下の領域を引けばよいですね。
Kp=0から0.83までの領域は右半分確率0.5からKp=0.83以上の領域を引けばよいですね。
よって答えは　(0.5-0.0485)+(0.5-0.2033)=0.7198
1000人あたりでは719人とわかりますね。

これも同様にして解けます。平均μと標準偏差σを求める必要があります。

3つのテーマで考えます。

★ 問題

不思議な問題文で、サイコロ１回振った結果は一様分布なのに、その回数を増やすと正規分布と異なる分布に変化していきます。

★ 解法(1回の場合)

確率を計算すると

となり、グラフも確かに一様分布ですね。当たり前ですよね、すべて等確率なので。

★ 解法(2回の場合)

確率を計算すると

となり、グラフは分布するようになってきましたが、まだ正規分布っぽくはないですね。

★ 解法(3回以上の場合)

さすがに手計算では大変なので、プログラムを使って計算してきましょう。
VBAプログラムを紹介して、これを使って計算してみます。

★ VBAプログラムイメージ

VBAプログラムの一例です。これを使ってサイコロ１回から６回までを計算します。７回以上はExcelで計算すると時間がかかるため、６回までとします。

★リンク【VBAプログラム】

実際に計算した結果をグラフにまとめると

グラフからわかるのは、

となりますね。不思議ですね。

なぜ、一様分布を重ねると徐々に正規分布へと異なる分布に変わるのか？はある程度数式で読み取れます。が、場合分けがたくさんあるので、手計算ではちょっと大変です。その１例を挙げます。

★１回から２回への変化

関連記事のように、畳み込み積分を使って計算します。

畳み込み積分がよくわかる(一様分布どうし) 畳み込み積分のイメージを高校数学を使ってわかりやすく解説し、さらに一様分布を使った畳み込み積分の計算の途中経過を一切端折らずに解説!

★畳み込み積分で分布が変わるところを理解する

例題を挙げると、

関連記事でおさえたいポイントは

この結果、一様分布から折れ線のような分布に変化します。

これを繰り返すと、一様分布から正規分布に近づく説明を数式で表現すればOKです。でも、場合分けが大変すぎるので、やり方だけ理解しておきましょう。

本記事では、一般的な正規分布を標準化する理由を解説し、一般の正規分布における任意の区間の確率を１つの方法で解ける解法を紹介しました。

★ 本記事のテーマ

★記事の信頼性

記事を書いている私は、QC検定®１級合格し、つまずきやすいQC検定®2級挑戦者に難解な確率密度関数をわかりやすく解説しています。

正規分布の理解を深めるための関連記事を紹介します。眺めて、慣れて、手で計算して習得しましょう。
●【初心者必見】正規分布の標準化や応用問題は怖くない！必勝解法を解説します。
●【簡単】正規分布は怖くない！正規分布表や確率計算の求め方がすぐわかる
●【簡単】確率分布関数がすぐ身につく方法
●【簡単】統計学最初の関門「平方和」がマスターできる【初心者向け】
●【簡単】高校数学で十分できる二項分布【初心者向け】
●基本統計量の演習問題【QC検定®2級対策】
●確率変数の期待値と分散が計算できる【初心者向け】

さっそく見ていきましょう。

●You tube動画もご確認ください。

世の中のデータや分布をグラフにまとめると、

のような分布が綺麗とされています。

身長、体重、試験点数などを分布にとると、綺麗な分布になりますよね。
数学的に証明されていませんが、多くのデータが不思議と正規分布にのります。

経験的に、社会現象、生物などのデータをとってきた結果、綺麗な分布な正規分布に従うことがおおいため、正規分布が確率密度関数の中心的存在となっています。
だから、教科書で最初に習う関数なのです。

正規分布の「正規」とは何か？　理想的？　中心的？　など気になりますが、
「正規」に意味はありません。正規分布を英語にすると「normal distribution」です。
正規分布とは、標準的「normal」な確率密度関数です。

確率密度関数は難しいイメージがありますが、y=ax+bやy=\(x^2\)などの簡単な関数でも良いです。

ただし、【簡単】確率分布関数がすぐ身につく方法で解説したように、区間[-∞,∞]で定積分∫f(x)dxが有限値を取り、なめらかである必要があります。

よって、指数関数などの難しい式になります。

正規分布関数の難しい式を見る前に、正規分布関数の特徴をおさえましょう。

特徴１については平均がμ、分散\(σ^2\)と一般型にできますが、本記事では簡単のため平均0、分散\(1^2\)で解説します。なお、平均（期待値E）と分散Vは次の式で計算できます。
期待値E,分散Vを積分から算出する過程も慣れてください。

$$ E= \int xf(x) dx $$
$$ V=\int x^2f(x) dx -E^2 $$

【簡単】確率分布関数がすぐ身につく方法で解説したように、y軸対称で平均0、分散\(1^2\)な関数は正規分布以外にもあります。

$$ f(x)=\frac{1}{4} e^{-|x|} $$

です。期待値E=0,分散V=1になります。しかし、\(e^{-x}\)型は尖っていて、なめらかではないため、あまり使いません。正規分布の関数より簡単な式なのに、残念！

なめらかな形状が必要な理由は、高い山をイメージすればわかります。例えば富士山の山頂は尖って要らずなめらかですよね。頂上ほど大気などによって削られてなめらかになります。多くのデータも中心付近でなめらかになります。

正規分布の関数の最大に弱点が、不定積分が求められないことです。つまり、
\(\int e^{-x^2}\)=??
なのです。

大学数学を駆使すれば定積分
\( \int_{-∞}^∞ f(x)dx\)
は計算できます。

不定積分がなければ、求めたい区間の積分値が計算できません。

正規分布表の使い方を理解する前に、区間の定積分が計算できないから表があることを理解しましょう。

なお、なめらかさを取らずに、正規分布関数を
\( f(x)=\frac{1}{4} e^{-|x|} \)
にすれば、区間の定積分が簡単に計算できます。この場合、正規分布表は不要ですね。

近似値として積分値を求めるイメージを紹介します。

赤線部dSの面積を求めます。曲線とはいえ、微小な領域を小さくすれば、面積dSはほぼ台形として近似して良いです。
図では例として、x=0.14と0.15の区間の面積dSとして台形の面積を求めます。
実際はx=0.14と0.15と差0.01よりもっと細かくして微小面積dSを求めていきます。

数値計算やシミュレーションでは積分できないものは細かく細分化して台形の面積としてかき集めることをやります。

確率は確率密度関数から面積(積分)で求めることがイメージできない方は、

【簡単】確率分布関数がすぐ身につく方法を読んでください。

確率密度関数は、変数xの区間[a,b]に発生する確率を算出したり、全体の分布がわかる便利な関数です。
また、確率密度関数の全区間の積分値は全確率１になります。

面積(積分)の計算が楽になるように、確率密度関数を簡単な式にしたいのですが、変な式ばかりなのが現実です。これが苦手意識につながります。苦手な人はイメージだけ持ってください。計算は世の中の数学が好きな人にお願いしましょう。

正規分布表はKpとpから値を読み取ります。ただの数表と思わず、面積で考えるイメージを持ってください。

正規分布表は下の図の青部の面積とそのxの位置を数値化したものです

まず縦にxに相当するKpがあります。正規分布は正負対称のグラフなので、正(x≧0)のみ表があれば十分です。例えば、Kp=1.96の時は確率P=0.05ですが、Kp=-1.96の時も同じ確率P=0.05です。

次に確率Pを見ます。確率PはKpが０の時は図3の左図のように1の半分の0.5と最大になりますが、Kpが大きくなるにつれて確率Pは小さくなります。表で見ると確率Pは上が大で下に行くにつれて確率Pは小になります。正規分布のグラフをイメージしましょう。

最後に表の横の流れを見ます。表の横は、Kpの0.01の桁とそれに対応する確率Pの値が書いており、横の流れは微調整程度と理解してください。本来はKpの値ですから縦に並べるべきですが、表が縦長になるため、0.01桁は横に流しているわけです。

★よく使う正規分布表の値

・Kp=0.00の時は確率P=0.5ですね。
・片側検定でよく使うP=0.05のときのKp=1.645。
・両側検定でよく使うP=0.025(=0.05/2)のときのKp=1.96
表の見方を暗記するのではなく、関数のグラフをよく見て理解しましょう。

正規分布表の見方がわかれば、おしまいではなく、慣れたころにも再度ここに戻ってきてください。
なぜ正規分布表があるのか？説明できますか？　それは積分計算が大変だからです。
正規分布表の使い方という手段だけでなく、正規分布表が必要な意味や目的も理解しましょう。

本記事では、正規分布がよく活用される背景や、分布の特徴、正規分布表の存在意義や使い方を解説しました。計算だけでなくグラフ、面積、確率を図でイメージすることが重要です。

正規分布の理解を深めるための関連記事を紹介します。眺めて、慣れて、手で計算して習得しましょう。
●【初心者必見】正規分布の標準化や応用問題は怖くない！必勝解法を解説します。
●【簡単】正規分布は怖くない！正規分布表や確率計算の求め方がすぐわかる
●【簡単】確率分布関数がすぐ身につく方法
●【簡単】統計学最初の関門「平方和」がマスターできる【初心者向け】
●【簡単】高校数学で十分できる二項分布【初心者向け】
●基本統計量の演習問題【QC検定®2級対策】
●確率変数の期待値と分散が計算できる【初心者向け】

★ 本記事のテーマ

★ QC模試受験しよう！

ＱＣ模試（品質技量の腕試し＆QC検定®対策） 品質技量の実力を試したい！ QC検定®合格対策に活用したい！オリジナル試験問題を提供します！

★【QC検定® 2級合格対策講座】で必勝！

QC検定® 2級合格対策講座を販売します。合格だけでなく、各単元の本質も理解でき、QC検定® 1級合格も狙える５９題をぜひ活用ください。

★【必勝メモ】と【必勝ドリル】のご紹介

試験合格に必要最小限エッセンスをまとめた「必勝メモ」と
何度も解いて合格に導く「必勝ドリル」
何度も繰り返すから力になる！

a		a		a
a		a		a
a		a		a
QC検定®２級必勝メモ 1000円		QC検定®２級必勝ドリル 1000円

★品質管理(ＱＣ)を究める数理問題集(初級・中級向け)

QC検定®3級、QC検定®2級受験の方、QC検定®１級受験挑戦する方への問題集(80問)です。
数学が苦手で品質管理の数理で苦戦していたら是非勉強しましょう！

a		a
a		a
a		a
品質管理(ＱＣ)を究めるを 数理問題集 (初級・中級向け) 3000円

母集団と標本データの違いを説明します。母集団とはデータ全体であり、標本とは母集団から一部を取り出したものですね。

具体例も紹介します。

母集団は20代の日本人全員のデータを集めるのはムリですね。全員見つけるのは大変ですし、常に人数は増減します。だから、現実に評価可能な範囲の人数を②標本として調べますよね。

また、標本データに興味はなく、標本から母集団の様子を推定したいはずです。
なので、標本から母集団を推定するデータ解析が必要になります。それは平均と分散なわけです。

標本から取り出せる平均は「標本平均」、分散は「標本分散」と呼んでいます。

2つのニーズがあります。

値を定義します。

では、標本と母集団の平均と分散の関係を調べましょう。

平均と分散についてそれぞれ標本と母集団との関係式を見てみましょう。

E[\(\bar{x}\)]
=E[\(\frac{1}{n}(x_1+x_2+…+x_n\)]
=\(\frac{1}{n}\)(E[\(x_1\)]+ E[\(x_2\)]+…+ E[\(x_n\)])
=\(\frac{1}{n}\)(μ+μ+…+μ)
= \(\frac{1}{n}\)nμ
=μ

となり、標本平均の期待値は母平均と一致します。

なお、E[\(x_i\)]=μを使っています。
各サンプルの平均の推定値である母平均はすべてμになるはずと期待しているからです。