「抜取検査を2回する場合のOC曲線が描けない」、「2回抜取方式の場合のロット合格率L(p)の計算がわからない」など困っていませんか?
こういう疑問に答えます。
本記事のテーマ
2回抜取方式(ポアソン分布)のOC曲線を作る
- ①2回抜取方式のロット合格率の計算
- ②2回抜取方式のロット合格率の公式導出
- ③2回抜取方式のOC曲線
- ④1回抜取と2回抜取のOC曲線比較
- ⑤⑤2回抜取方式は検査量が減らせるメリットがある
本物の「抜取検査」問題集を販売します!
 |
今回、【QC検定®合格】「抜取検査」問題集を販売します! 内容は、①二項分布・ポアソン分布、OC曲線、➁多回抜取検査、➂選別型抜取検査、➃計量抜取検査、⑤逐次抜取検査、⑥調整型抜取検査、⑦抜取検査まとめ の7章全47題を演習できる問題集です。しっかり勉強しましょう。 |
①2回抜取方式のロット合格率の計算
具体例を計算してから、公式導出します。
1回目試料数n1=50個、合格判定ac1=1個、不合格判定re1=3個
2回目試料数n2=50個、合格判定ac2=4個、不合格判定re2=5個
合格基準を詳しくみます!
(A)1回目の抜取検査で、不良数が1個(ac1個)以内なら、1回の抜取検査で合格し終了!
(B)1回目の抜取検査で、不良数が2個(ac1+1個以上、re1-1個以下)なら、2回目の検査を実施。
2回目の検査で、不良数がトータル4個以下なら検査は合格、5個以上なら不合格で終了!
(C) (A)(B)以外はすべて不合格
検査合格条件を表にまとめます。
| 1回目 | 2回目 |
| 0個 | 検査不要 |
| 1個 | 検査不要 |
| 2個 | 0個 |
| 1個 | |
| 2個 |
まとめると、
●1回目の不良数が1個以下なら、検査は1回で合格と
●1回目の不良数が2個の場合、2回目の不良数が0~2個なら検査は合格
となります。
ここから
ロット合格率L(p)を計算します。
「1回目の不良数が1個以下なら、検査は1回で合格と
1回目の不良数が2個の場合、2回目の不良数が0~2個なら検査は合格
となります。」
を式で書けばOKです。
ポアソン分布の式を代入が難しいので、丁寧に解説します。
L(p=0.02)= \(\sum_{r=0}^{1} exp(-λ_1)\frac{λ_1^r}{r!}\)
+ \(\sum_{r=2}^{2}\){\( exp(-λ_1)\frac{λ_1^r}{r!}\)
× \(\sum_{s=0}^{2} exp(-λ_2)\frac{λ_2^r}{r!}\)}
=0.98514
ここで、
λ1=n1×p=50×0.01=0.5
λ2=n2×p=50×0.01=0.5
数式が難しいですが、1つずつ見ましょう。
\(\sum_{r=0}^{1} exp(-λ_1)\frac{λ_1^r}{r!}\)は,1回目の不良数が1個以下なら、検査は1回で合格の場合です。
\(\sum_{r=2}^{2}\)\( exp(-λ_1)\frac{λ_1^r}{r!}\)は、1回目の不良数が2個の場合で、
\(\sum_{s=0}^{2} exp(-λ_2)\frac{λ_2^r}{r!}\)は、2回目の不良数が0~2個の場合です。
1回目と2回目と連続で検査するので確率の積となります。
②2回抜取方式のロット合格率の公式導出
上の例題にある数字を文字に変えます。
1回目試料数n1個、合格判定ac1個、不合格判定re1個
2回目試料数n2個、合格判定ac2個、不合格判定re2個
上の例題を解く数式は、
L(p=0.02)= \(\sum_{r=0}^{1} exp(-λ_1)\frac{λ_1^r}{r!}\)
+ \(\sum_{r=2}^{2}\){\( exp(-λ_1)\frac{λ_1^r}{r!}\)
× \(\sum_{s=0}^{2} exp(-λ_2)\frac{λ_2^r}{r!}\)}
数字を文字に変えます。
L(p)= \(\sum_{r=0}^{ ac1} exp(-λ_1)\frac{λ_1^r}{r!}\)
+ \(\sum_{r=ac1+1}^{re1-1}\){\( exp(-λ_1)\frac{λ_1^r}{r!}\)
× \(\sum_{s=0}^{ac2-r} exp(-λ_2)\frac{λ_2^r}{r!}\)}
この式の難しいところは、
①\(\sum_{r=ac1+1}^{re1-1}\)と②\(\sum_{s=0}^{ac2-r}\)ですね。
①2回目の検査が必要な場合は、1回目で出る不良数がac1+1個以上、re1-1個ですね。
②すでに1回目でr個(ac1+1≦r≦re1-1)不良を出しているので、
2回目で出してもいい不良数は ac2-r個になります。
③2回抜取方式のOC曲線
2回抜取方式のOC曲線の式は、
L(p)= \(\sum_{r=0}^{ ac1} exp(-λ_1)\frac{λ_1^r}{r!}\)
+ \(\sum_{r=ac1+1}^{re1-1}\){\( exp(-λ_1)\frac{λ_1^r}{r!}\)
× \(\sum_{s=0}^{ac2-r} exp(-λ_2)\frac{λ_2^r}{r!}\)}
1回目試料数n1=50個、合格判定ac1=1個、不合格判定re1=3個
2回目試料数n2=50個、合格判定ac2=4個、不合格判定re2=5個
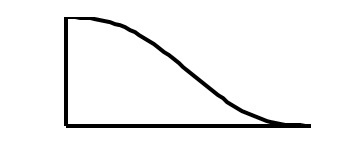
を代入してOC曲線を描くと下図のようになります。

1回抜取方式のOC曲線と似た曲線になります。
④1回抜取と2回抜取のOC曲線比較
1回目試料数n1=50個、合格判定ac1=1個、不合格判定re1=3個
2回目試料数n2=50個、合格判定ac2=4個、不合格判定re2=5個
(B)100個を1回抜取検査する場合
試料数n=100,合格判定c=4個
(合格判定不良個数は同じとする)
のOC曲線を比較しましょう。
OC曲線は関連記事のプログラムで自動作成できます。
 |
OC曲線(二項分布、ポアソン分布)を描こう 抜取検査はすべて、OC曲線をベースに考えます。OC曲線をすぐ描けるようプログラムを用意しました。二項分布、ポアソン分布両方のOC曲線を実際に描いて感触を確かめましょう。 |

これが、複数回に分けて抜取検査するメリットにつながります。
⑤2回抜取方式は検査量が減らせるメリットがある
2回抜取検査のうち、ほとんどが1回の検査で終了する
下図の黒線と青線は、
黒線:2回の抜取検査で合格するすべての場合を合算
青線:2回の抜取検査のうち、1回で合格する場合だけを合算
で区別しています。

青線と黒線の差が小さいことがわかります。
つまり、2回抜取検査と言いながら、多くの場合はn=50個の1回抜取検査で終了するのです。
1回抜取検査n=100個より少ない個数で抜取検査が終えることができます。
複数の抜取検査は平均検査量が減らせる
●2回抜取検査のうち、合格するすべての場合の確率p1
●1回で終わる場合の確率をp2(p2 > p1)とします。
検査量を計算
2回抜取検査の検査量の期待値を計算します。
●2回抜取検査の検査量の期待値=
1回で終わる場合の検査量の期待値+2回で終わる場合の検査量の期待値
です。
つまり、検査量の期待値Iは
I=p2/p1× n1 + (p1-p2)/p1 × (n1+n2)
です。
実際は、n1=50,n1+n2=100, p2/p1=0.8, (p1-p2)/p1=0.2くらいなので、
I= 0.8×50+ 0.2×100 = 60
となり、2回抜取検査の計100個より少ない60個くらいの検査で済むことがわかります。
つまり、検査量が減らせる効果があります。
でも、その逆に検査を複数回するのが面倒ではあります。
不良率と検査量の関係
2回抜取検査(n1=50,n2=50)と1回抜取検査(n=100)における検査量を比較しましょう。

2回抜取検査はある不良率pでピークを持ちますが、1回抜取検査より検査量が少ないことが分かります。
多回に検査を分けると、1,2回目の検査で検査の合否がほとんど決まるから、検査量の期待値が少ないわけです。
まとめ
抜取検査を2回する場合のポアソン分布を使った、ロット合格率L(p)の計算、OC曲線の描き方、1回抜取検査と2回抜取検査の比較をして、2回抜取検査の方が検査量が減らせるメリットがあることを解説しました。
- ①2回抜取方式のロット合格率の計算
- ②2回抜取方式のロット合格率の公式導出
- ③2回抜取方式のOC曲線
- ④1回抜取と2回抜取のOC曲線比較
- ⑤2回抜取方式は検査量が減らせるメリットがある